NOTE: Robustness reported in this article is being revised with corrections in derivative calculations. Updated results will be published shortly from these corrections.

Introduction

A natural approach of understanding an unknown model is to get some sample points from the model and use these points to build a response surface model (RSM) to represent the true model.

In this process, two factors play a vital role in RSM accuracy. One is the sampling points to use for building the model and the other is the selection and training of the model. Given so many choices of sampling methods and learning models, an inevitable question we are all asking is, which sampling type and learning model we should use. In this article, we will explore how different combinations of sampling methods and learning models affects the accuracy of the RSM model.

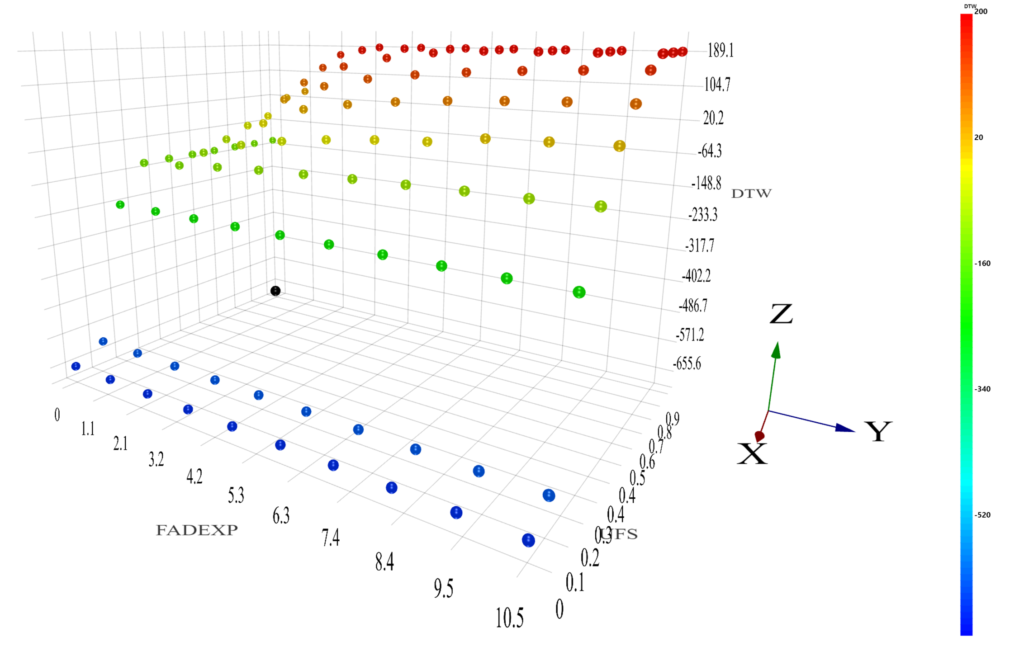
Dynamic Time Warping

We start with a reference FD curve generated from simulation using UFS = 0.4 and FADEXP = 8. We want to find a set of values for parameter UFS and FADEXP that generates a curve that will be very close to the reference curve we have. In order to compare the similarity of two curves, we use Dynamic Time Warping score (DTW) as a metric. If two curves are perfectly overlapping with each other, we get DTW = 0. Otherwise, two different curves will result in a non-zero DTW score that indicates how different the two curves are. A larger the DTW score implies larger difference.

Sampling and Learning

There are four main sampling types : Full Factorial Design (FFD), D-Optimal Design (DOPT), Latin Hypercube (LHS), and Space Filling (SF). In addition to these four basic designs, we can combine any two sampling types to get a new design. We will consider DLHS (a combination of DOPT and LHS design), DSF (a combination of DOP and SF design), and LS ( a combination of LHS and SF design). We sample 16 points for FFD, 4 points for DOPT, LHS, and SF. This will give us 8 points for DLHS, DSF, and LS.

FFD points are evenly distributed in the design space. DOPT points occupy the four corners. LHS has at least one point that can represent each region of the design space. Comparing to DOPT points, LHS points gather more information about the design space. SF points are not as scattered as LHS points, but better than DOPT points.

We use these points to learn machine learning models to be used as RSM. A brief description of the ML models considered are listed below.

With sampling points and choice of model, we can build a RSM model. Using this RSM model, we can find the optimal point whose DTW score is closest to zero.

Error Estimation

In order to evaluate the performance of each RSM model, we introduce 3 types of error : RSM Error, Optimal Prediction Error, and Robust Error.

RSM Error

We sample 100 points from the design space using FFD design. We run simulation on these 100 points and calculate their DTW score. These 100 points represent the true model. We call it FFD100.

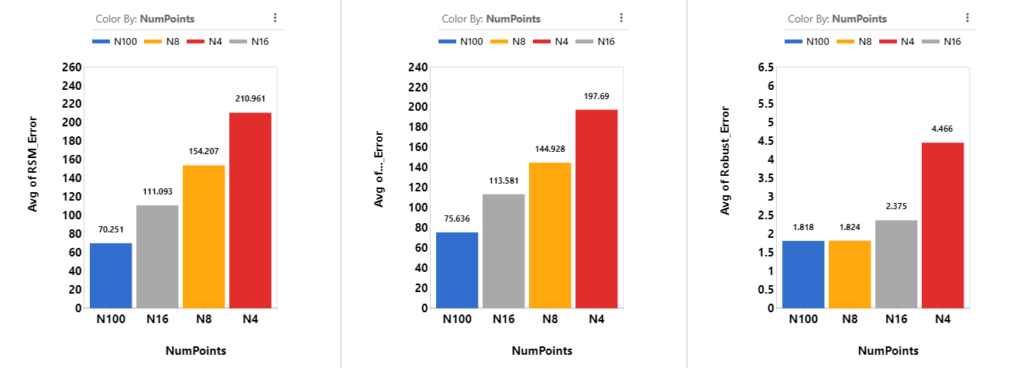
In order to evaluate the RSM models, we can compare them to the FFD100 model. We use the RSM model to make predictions of the DTW score on each point from FFD100, then we compare the predicted values against the simulation values. We average these errors (taking the absolute values) and we get the RSM Error.

Optimal Prediction Error

After we get the predicted values for the FFD100 sampling points, we use Pareto Front Optimizer to find out the optimal point having the closest DTW score to zero. Comparing the simulation DTW score and the predicted DTW score at this point, we get the Optimal Prediction Error (taking the absolute value).

Robust Error

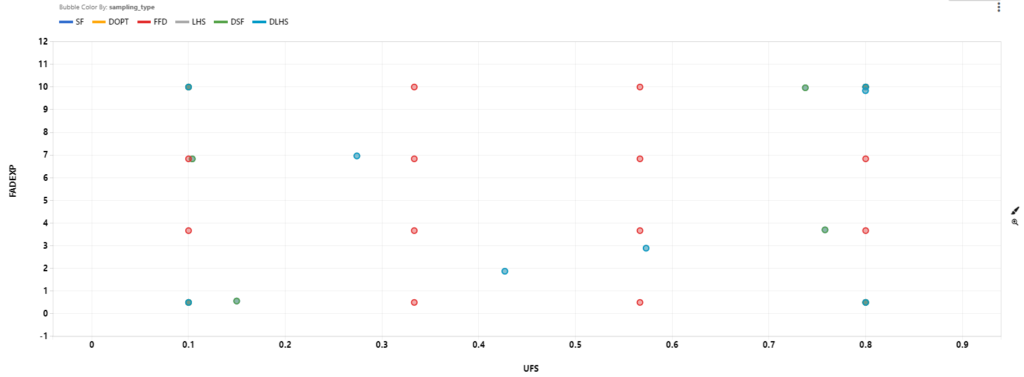
In order to study the robustness, we find 4 adjacent points around the optimal point we found from each RSM model. Then, we get the simulation DTW score for these adjacent points and we compare them to the simulation DTW score at the optimal point. Taking the average of these errors (taking the absolute values), we get the Robust Error.

Result

Generally speaking, more sampling points means we have more information on the true model, and thus the RSM model we build based on these sampling points also have lower errors. This can be confirmed with the average RSM Error and Optimal Prediction Error. Both of these two errors are calculated by comparing simulation and predicted DTW scores. On the other hand, Robust Error comes from comparing simulation DTW scores. Thus, it doesn’t share the trend.

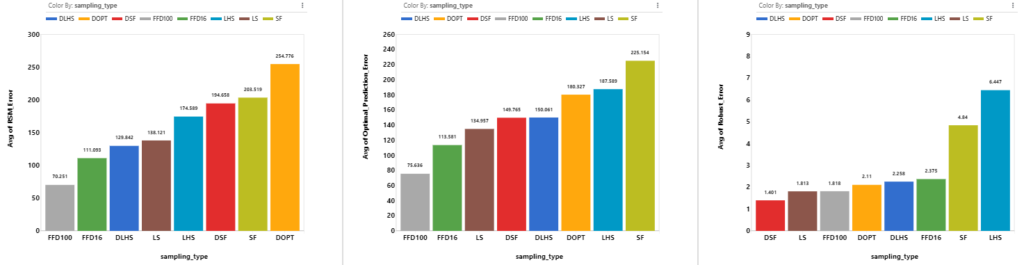
Since sampling type is associated with the number of points, it is expected that designs with more points will have lower errors. Excluding FFD designs, we see that LS has lower RSM Error, Optimal Prediction Error and Robust Error.

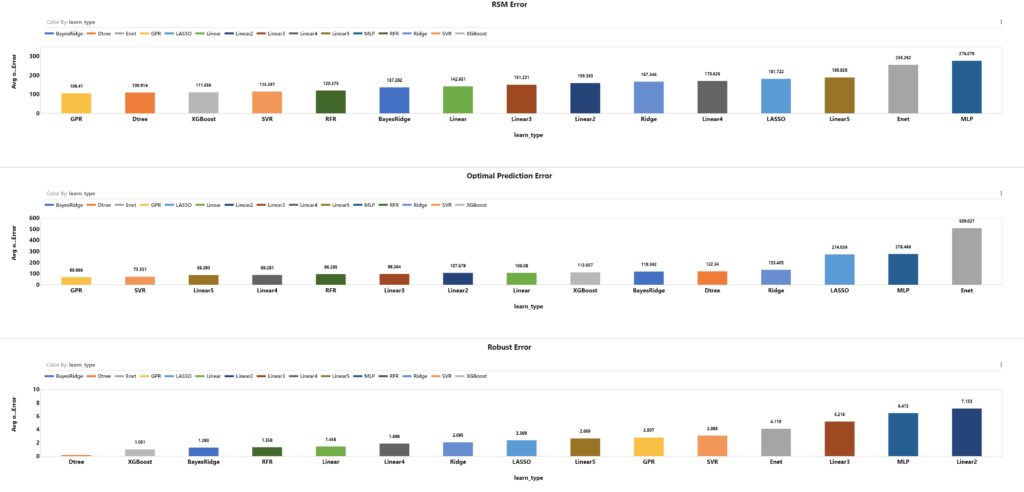
Based on learning type, the difference of top models are not very significant. GPR, SVR, RFR perform well in terms of RSM Error and Optimal Prediction Error. Dtree, XGBoost, BayesRidge and RFR models perform well in Robust Error.

From the scatter plot of the RSM Error and Optimal Prediction Error, we can see a general trend that higher RSM Error is associated with higher Optimal Prediction Error. This is true for all sampling type. However, when we take a closer look at each sampling type, it is noticeable that the top RSM models (with low RSM Error and Optimal Prediction Error) doesn’t show a very clear correlation between the two errors.

Meanwhile, RSM Error and Robust Error don’t seem to be related at all.

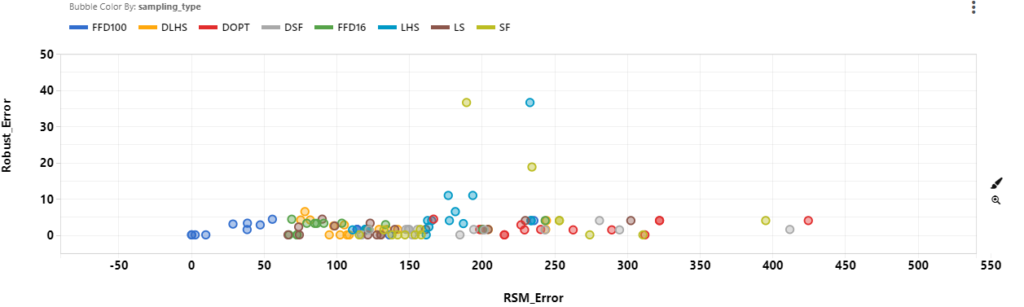
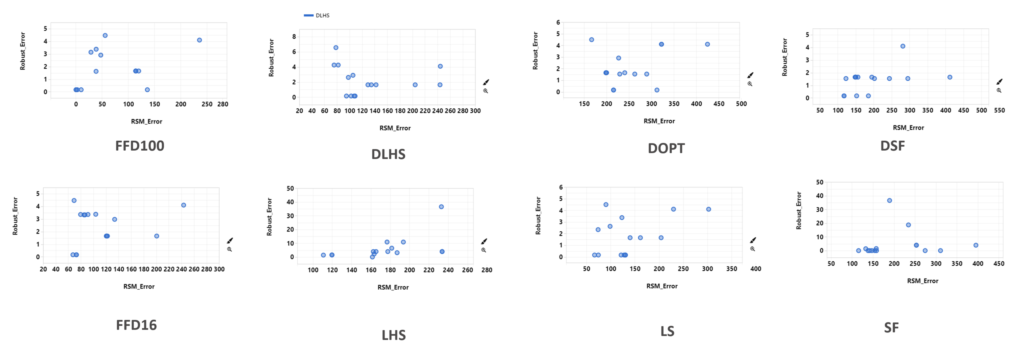
We are interested in a combination of sampling type and learning type using the least number of points that will have the lowest errors. Pareto Front Optimizer uses these criteria and assigns a distance score (dist) to each of the RSM model based on how far away they are from the ideal point (a point with the lowest errors and least number of points).

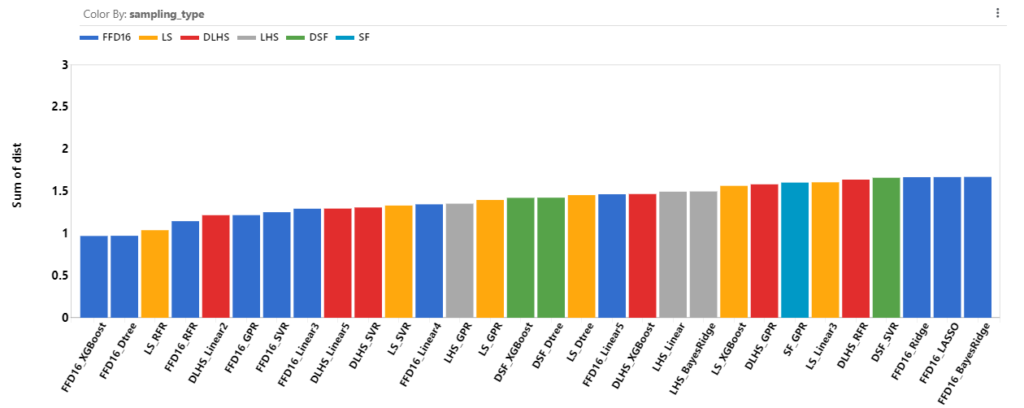
From the errors, LS performs the best. Looking at the distance score, we see LS points with any of the XGBoost, Dtree, RFR, GPR, SVR learning models perform very well comparing to the other RSM models .

Conclusion

Each sampling type has their unique characteristics. Combining with different learning types, we get some very useful RSM models. Among these models, LS combined with XGBoost, Dtree, RFR, SVR and GPR as their learning model generally have a more accurate and robust RSM model.