In any wave propagation code, such as LS-DYNA, which belongs to a family of ‘Hydro’ codes, bulk viscosity is essential to treat shocks. Smooth initial data can lead into shock discontinuities and if left untreated can result in severe instabilities. LS-DYNA has the capability (performed by default) to automatically detect the shocks and treat them by adding a pressure term that is based on the element dimension, density, strain-rate and some user-defined coefficients (Q1 and Q2). The addition of the pressure term guarantees unperturbed solution away from the shock and satisfies Hugoniot jump conditions that requires the conservation of mass, momentum and energy across the shock front. The automatic detection of the shock was originally performed by looking at the divergence of the velocity field which is now replaced with the trace of the strain-rate tensor in multidimensional problems. The divergence of a vector field such as a velocity shows us the amount of flux or density that is flowing in (sink or compression or convergence) or out of (source or expansion or divergence) of a certain area. The divergence of a vector field provides us with a scalar function whose values are positive for out-flow (source, expansion,divergence) and negative (sink, compression, convergence). Fortunately, in multi-dimensions, the trace of a strain-rate tensor provides us this information very easily which is computed every cycle by LS-DYNA. If the trace of the strain-rate tensor is negative (compression, convergence, sink), then LS-DYNA automatically adds a pressure them that is based on the element dimension (square-root of Area for 2D and cube-root of Volume for 3D) while a positive trace is ignored.
Bulk Viscosity Coefficients
LS-DYNA provides two types of bulk viscosity coefficients namely Q1 and Q2. Q1 is called as the quadratic term that helps to smear the shocks and also helps in preventing the element from collapsing under high velocities where the particle velocity is exceeds the sounds speed for the material. Q2 which is called as the linear term, helps to rapidly damp out the oscillations, often called as the ‘ringing’. By default, these coefficients are fixed at 1.5 (Q1) and 0.06 (Q2) and are both active for solid elements. Starting 970, LS-DYNA allows the application of the bulk viscosity pressure for shell elements which can be invoked by setting TYPE = -2 in *CONTROL_BULK_VISCOSITY. Use of bulk viscosity for shells and solids are highly recommended to improve simulation stability. The internal energy that is dissipated by viscosity is computed and included in the overall energy balance.
Simple Elastic Impact Example
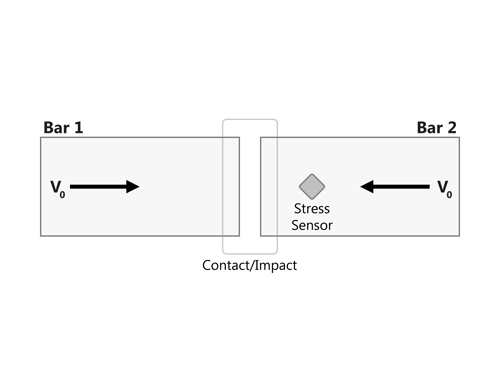
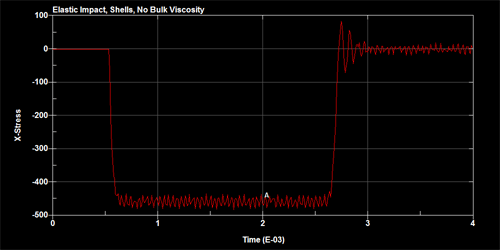
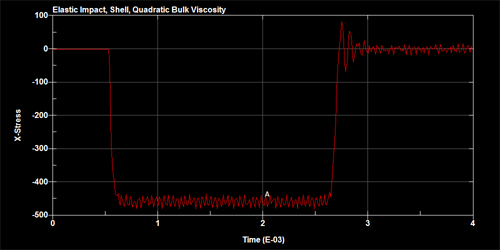
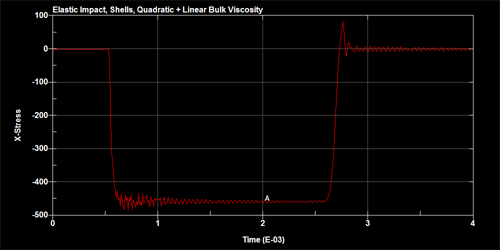
To demonstrate the effects of the adding the bulk viscosity, two slender bars are set up to impact against each other as shown in figure below. The bars are meshed using shells and a single element away from the point of impact is monitored for the uni-axial stress time history. The figures below show the stress time history for no bulk viscosity, quadratic bulk viscosity and quadratic+linear bulk viscosity.
(Click image to enlarge)
(Click image to enlarge)
(Click image to enlarge)
(Click image to enlarge)
References:
1. LS-DYNA Theory Manual, 2007, Livermore Software Technology Corp.
2. LS-DYNA Keyword Manual, 2007, Livermore Software Technology Corp.
Acknowledgement:
Jim Day for reviewing this post and providing valuable comments and suggestions
